I’ve been interested in functional reactive programming (FRP) for about a decade now. I even wrote a couple of blog posts back in 2014 describing my experiments. My initial source of inspiration was Elm, the Haskell-like language for the web that once had FRP as a core part of the language. Evan Czaplicki’s Strange Loop 2013 talk really impressed me, especially that Mario demo. From there, I explored the academic literature on the subject.
Ultimately, I created and then abandoned a library that focused on FRP for games. It was a neat idea, but the performance was terrible. The overhead of my kinda-sorta FRP system was part of the problem, but mostly it was my own inexperience. I didn’t know how to optimize effectively and my implementation language, Guile, did not have as many optimization passes as it does now. Also, realtime simulations like games require much more careful use of heap allocation.
I found that, overhead aside, FRP is a bad fit for things like scripting sequences of actions in a game. I don’t want to give up things like coroutines that make it easy. I’ve learned how different layers of a program may call for different programming paradigms. Functional layers rest upon imperative foundations. Events are built on top of polling. Languages with expression trees run on machines that only understand linear sequences. You get the idea. A good general-purpose language will allow you to compose many paradigms in the same program. I’m still a big fan of functional programming, but single paradigm languages do not appeal to me.
Fast forward 10 years, I find myself thinking about FRP again in a new context. I now work for the Spritely Institute where we’re researching and building the next generation of secure, distributed application infrastructure. We want to demo our tech through easy-to-use web applications, which means we need to do some UI programming. So, the back burner of my brain has been mulling over the possibilities. What’s the least painful way to build web UIs? Is this FRP thing worth revisiting?
The reason why FRP is so appealing to me (on paper, at least) is that it allows for writing interactive programs declaratively. With FRP, I can simply describe the relationships between the various time-varying components, and the system wires it all together for me. I’m spared from callback hell, one of the more frightening layers of hell that forces programs to be written in a kind of continuation-passing style where timing and state bugs consume more development time as the project grows.
What about React?
In the time during and since I last experimented with FRP, a different approach to declarative UI programming has swept the web development world: React. From React, many other similar libraries emerged. On the minimalist side there are things like Mithril (a favorite of mine), and then there are bigger players like Vue. The term “reactive” has become overloaded, but in the mainstream software world it is associated with React and friends. FRP is quite different, despite sharing the declarative and reactive traits. Both help free programmers from callback hell, but they achieve their results differently.
The React model describes an application as a tree of “components”. Each component represents a subset of the complete UI element tree. For each component, there is a template function that takes some inputs and returns the new desired state of the UI. This function is called whenever an event occurs that might change the state of the UI. The template produces a data structure known as a “virtual DOM”. To realize this new state in the actual DOM, React diffs the previous tree with the new one and updates, creates, and deletes elements as necessary.
With FRP, you describe your program as an acyclic graph of nodes that contain time-varying values. The actual value of any given node is determined by a function that maps the current values of some input nodes into an output value. The system is bootstrapped by handling a UI event and updating the appropriate root node, which kicks off a cascade of updates throughout the graph. At the leaf nodes, side-effects occur that realize the desired state of the application. Racket’s FrTime is one example of such a system, which is based on Greg Cooper’s 2008 PhD dissertation “Integrating Dataflow Evaluation into a Practical Higher-Order Call-by-Value Language”. In FrTime, time-varying values are called “signals”. Elm borrowed this language, too, and there’s currently a proposal to add signals to JavaScript. Research into FRP goes back quite a bit further. Notably, Conal Elliot and Paul Hudak wrote “Functional Reactive Animation” in 1997.
On jank
The scope of potential change for any given event is larger in React than FRP. An FRP system flows data through an acyclic graph, updating only the nodes affected by the event. React requires re-evaluating the template for each component that needs refreshing and applying a diff algorithm to determine what needs changing in the currently rendered UI. The virtual DOM diffing process can be quite wasteful in terms of both memory usage and processing time, leading to jank on systems with limited resources like phones. Andy Wingo has done some interesting analyses of things like React Native and Flutter and covers the subject of jank well. So, while I appreciate the greatly improved developer experience of React-likes (I wrote my fair share of frontend code in the jQuery days), I’m less pleased by the overhead that it pushes onto each user’s computer. React feels like an important step forward on the declarative UI trail, but it’s not the destination.
FRP has the potential for less jank because side-effects (the UI widget state updates) can be more precise. For example, if a web page has a text node that displays the number of times the user has clicked a mouse button, an FRP system could produce a program that would do the natural thing: Register a click event handler that replaces the text node with a new one containing the updated count. We don’t need to diff the whole page, nor do we need to create a wrapper component to update a subset of the page. The scope is narrow, so we can apply smaller updates. No virtual DOM necessary. There is, of course, overhead to maintaining the graph of time-varying values. The underlying runtime is free to use mutable state, but the user layer must take care to use pure functions and persistent, immutable data structures. This has a cost, but the per-event cost to refresh the UI feels much more reasonable when compared to React. From here on, I will stop talking about React and start exploring if FRP might really offer a more expressive way to do declarative UI without too much overhead. But first, we need to talk about a serious problem.
FRP is acyclic
FRP is no silver bullet. As mentioned earlier, FRP graphs are typically of the acyclic flavor. This limits the set of UIs that are possible to create with FRP. Is this the cost of declarativeness? To demonstrate the problem, consider a color picker tool that has sliders for both the red-green-blue and hue-saturation-value representations of color:
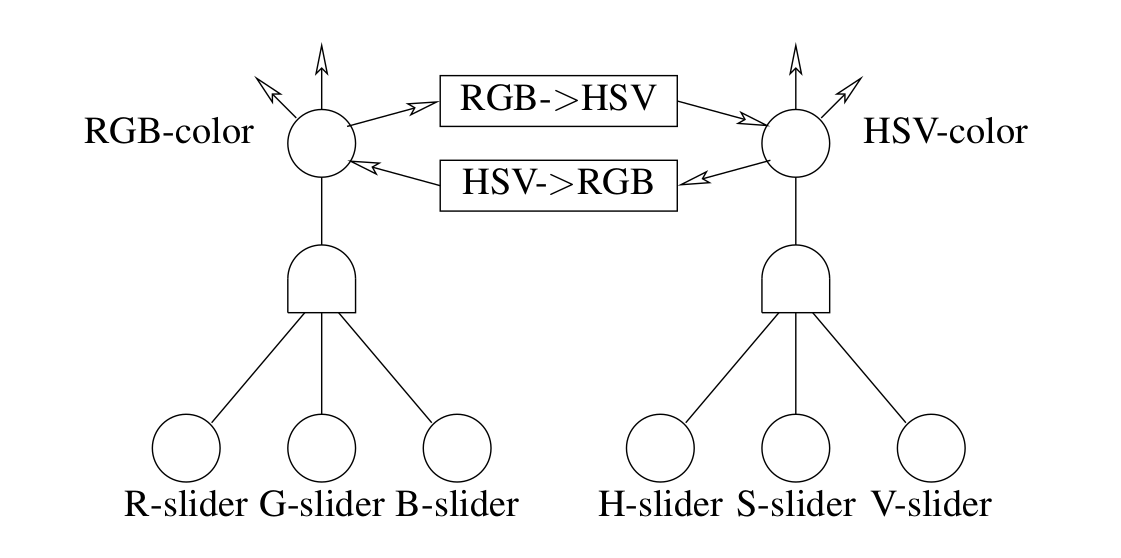
In this program, updating the sliders on the RGB side should change the values of the sliders on the HSV side, and vice versa. This forms a cycle between the two sets of sliders. It’s possible to express cycles like this with event callbacks, though it’s messy and error-prone to do manually. We’d like a system built on top of event callbacks that can do the right thing without strange glitches or worse, unbounded loops.
Propagators to the rescue
Fortunately, I didn’t create that diagram above. It’s from Alexey Radul’s 2009 PhD dissertation: “Propagation Networks: A Flexible and Expressive Substrate for Computation”. This paper dedicates a section to explaining how FRP can be built on top a more general paradigm called propagation networks, or just propagators for short. The paper is lengthy, naturally, but it is written in an approachable style. There isn’t any terse math notation and there are plenty of code examples. As far as PhD dissertations go, this one is a real page turner!
Here is a quote from section 5.5 about FrTime (with emphasis added by me):
FrTime is built around a custom propagation infrastructure; it nicely achieves both non-recomputation and glitch avoidance, but unfortunately, the propagation system is nontrivially complicated, and specialized for the purpose of supporting functional reactivity. In particular, the FrTime system imposes the invariant that the propagation graph be acyclic, and guarantees that it will execute the propagators in topological-sort order. This simplifies the propagators themselves, but greatly complicates the runtime system, especially because it has to dynamically recompute the sort order when the structure of some portion of the graph changes (as when the predicate of a conditional changes from true to false, and the other branch must now be computed). That complexity, in turn, makes that runtime system unsuitable for other kinds of propagation, and even makes it difficult for other kinds of propagation to interoperate with it.
So, the claim is that FRP-on-propagators can remove the acyclic restriction, reduce complexity, and improve interoperability. But what are propagators? I like how the book “Software Design for Flexibility” (2021) defines them (again, with emphasis added by me):
“The propagator model is built on the idea that the basic computational elements are propagators, autonomous independent machines interconnected by shared cells through which they communicate. Each propagator machine continuously examines the cells it is connected to, and adds information to some cells based on computations it can make from information it can get from others. Cells accumulate information and propagators produce information.”
Research on propagators goes back a long way (you’ll even find a form of propagators in the all-time classic “Structure and Interpretation of Computer Programs”), but it was Alexey Radul that discovered how to unify many different types of special-purpose propagation systems so that they could share a generic substrate and interoperate.
Perhaps the most exciting application of the propagator model is AI, where it can be used to create “explainable AI” that keeps track of how a particular output was computed. This type of AI stands in stark contrast to the much hyped mainstream machine learning models that hoover up our planet’s precious natural resources to produce black boxes that generate impressive bullshit. But anyway!
The diagram above can also be found in section 5.5 of the dissertation. Here’s the description:
“A network for a widget for RGB and HSV color selection. Traditional functional reactive systems have qualms about the circularity, but general-purpose propagation handles it automatically.”
This color picker felt like a good, achievable target for a prototype. The propagator network is small and there are only a handful of UI elements, yet it will test if the FRP system is working correctly.
The prototype
I read Alexey Radul’s dissertation, and then read chapter 7 of Software Design for Flexibility, which is all about propagators. Both use Scheme as the implementation language. The latter makes no mention of FRP, and while the former explains how FRP can be implemented in terms of propagators, there is (understandably) no code included. So, I had to implement it for myself to test my understanding. Unsurprisingly, I had misunderstood many things along the way and my iterations of broken code let me know that. Implementation is the best teacher.
After much code fiddling, I was able to create a working prototype of the color picker. Here it is below:
This prototype is written in Scheme and uses Hoot to compile it to WebAssembly so I can embed it right here in my blog. Sure beats a screenshot or video! This prototype contains a minimal propagator implementation that is sufficient to bootstrap a similarly minimal FRP implementation.
Propagator implementation
Let’s take a look at the code and see how it all works, starting with propagation. There are two essential data types: Cells and propagators. Cells accumulate information about a value, ranging from nothing, some form of partial information, or a complete value. The concept of partial information is Alexey Radul’s major contribution to the propagator model. It is through partial information structures that general-purpose propagators can be used to implement logic programming, probabilistic programming, type inference, and FRP, among others. I’m going to keep things as simple as possible in this post (it’s a big enough infodump already), but do read the propagator literature if phrases like “dependency directed backtracking” and “truth maintenance system” sound like a good time to you.
Cells start out knowing nothing, so we need a special, unique value to represent nothing:
(define-record-type <nothing>
(make-nothing)
%nothing?)
(define nothing (make-nothing))
(define (nothing? x) (eq? x nothing))Any unique (as in eq?) object would do, such as (list ’nothing),
but I chose to use a record type because I like the way it prints.
In addition to nothing, the propagator model also has a notion of contradictions. If one source of information says there are four lights, but another says there are five, then we have a contradiction. Propagation networks do not fall apart in the presence of contradictory information. There’s a data type that captures information about them and they can be resolved in a context-specific manner. I mention contradictions only for the sake of completeness, as a general-purpose propagator system needs to handle them. This prototype does not create any contradictions, so I won’t mention them again.
Now we can define a cell type:
(define-record-type <cell>
(%make-cell relations neighbors content strongest
equivalent? merge find-strongest handle-contradiction)
cell?
(relations cell-relations)
(neighbors cell-neighbors set-cell-neighbors!)
(content cell-content set-cell-content!)
(strongest cell-strongest set-cell-strongest!)
;; Dispatch table:
(equivalent? cell-equivalent?)
(merge cell-merge)
(find-strongest cell-find-strongest)
(handle-contradiction cell-handle-contradiction))The details of how a cell does things like merge old information with new information is left intentionally unanswered at this level of abstraction. Different systems built on propagators will want to handle things in different ways. In the propagator literature, you’ll see generic procedures used extensively for this purpose. For the sake of simplicity, I use a dispatch table instead. It would be easy to layer generic merge on top later, if we wanted.
The constructor for cells sets the default contents to nothing:
(define default-equivalent? equal?)
;; But what about partial information???
(define (default-merge old new) new)
(define (default-find-strongest content) content)
(define (default-handle-contradiction cell) (values))
(define* (make-cell name #:key
(equivalent? default-equivalent?)
(merge default-merge)
(find-strongest default-find-strongest)
(handle-contradiction default-handle-contradiction))
(let ((cell (%make-cell (make-relations name) '() nothing nothing
equivalent? merge find-strongest
handle-contradiction)))
(add-child! (current-parent) cell)
cell))The default procedures used for the dispatch table are either no-ops
or trivial. The default merge doesn’t merge at all, it just
clobbers the old with the new. It’s up to the layers on top to
provide more useful implementations.
Cells can have neighbors (which will be propagators):
(define (add-cell-neighbor! cell neighbor)
(set-cell-neighbors! cell (lset-adjoin eq? (cell-neighbors cell) neighbor)))Since cells accumulate information, there are procedures for adding new content and finding the current strongest value contained within:
(define (add-cell-content! cell new)
(match cell
(($ <cell> _ neighbors content strongest equivalent? merge
find-strongest handle-contradiction)
(let ((content* (merge content new)))
(set-cell-content! cell content*)
(let ((strongest* (find-strongest content*)))
(cond
;; New strongest value is equivalent to the old one. No need
;; to alert propagators.
((equivalent? strongest strongest*)
(set-cell-strongest! cell strongest*))
;; Uh oh, a contradiction! Call handler.
((contradiction? strongest*)
(set-cell-strongest! cell strongest*)
(handle-contradiction cell))
;; Strongest value has changed. Alert the propagators!
(else
(set-cell-strongest! cell strongest*)
(for-each alert-propagator! neighbors))))))))Next up is the propagator type. Propagators can be activated to create information using content stored in cells and store their results in some other cells, forming a graph. Data flow is not forced to be directional. Cycles are not only permitted, but very common in practice. So, propagators keep track of both their input and output cells:
(define-record-type <propagator>
(%make-propagator relations inputs outputs activate)
propagator?
(relations propagator-relations)
(inputs propagator-inputs)
(outputs propagator-outputs)
(activate propagator-activate))Propagators can be alerted to schedule themselves to be re-evaluted:
(define (alert-propagator! propagator)
(queue-task! (propagator-activate propagator)))The constructor for propagators adds the new propagator as a neighbor
to all input cells and then calls alert-propagator! to bootstrap it:
(define (make-propagator name inputs outputs activate)
(let ((propagator (%make-propagator (make-relations name)
inputs outputs activate)))
(add-child! (current-parent) propagator)
(for-each (lambda (cell)
(add-cell-neighbor! cell propagator))
inputs)
(alert-propagator! propagator)
propagator))There are two main classes of propagators that will be used: primitive propagators and constraint propagators. Primitive propagators are directional; they apply a function to the values of some input cells and write the result to an output cell:
(define (unusable-value? x)
(or (nothing? x) (contradiction? x)))
(define (primitive-propagator name f)
(match-lambda*
((inputs ... output)
(define (activate)
(let ((args (map cell-strongest inputs)))
(unless (any unusable-value? args)
(add-cell-content! output (apply f args)))))
(make-propagator name inputs (list output) activate))))We can use primitive-propagator to lift standard Scheme procedures
into the realm of propagators. Here’s how we’d make and use an
addition propagator:
(define p:+ (primitive-propagator +))
(define a (make-cell))
(define b (make-cell))
(define c (make-cell))
(p:+ a b c)
(add-cell-content! a 1)
(add-cell-content! b 3)
;; After the scheduler runs…
(cell-strongest c) ;; => 4It is from these primitive propagators that we can build more complicated, compound propagators. Compound propagators compose primitive propagators (or other compound propagators) and lazily construct their section of the network upon first activation:
(define (compound-propagator name inputs outputs build)
(let ((built? #f))
(define (maybe-build)
(unless (or built?
(and (not (null? inputs))
(every unusable-value? (map cell-strongest inputs))))
(parameterize ((current-parent (propagator-relations propagator)))
(build)
(set! built? #t))))
(define propagator (make-propagator name inputs outputs maybe-build))
propagator))By this point you may be wondering what all the references to
current-parent are about. It is for tracking the parent/child
relationships of the cells and propagators in the network. This could
be helpful for things like visualizing the network, but we aren’t
going to do anything with it today. I’ve omitted all of the other
relation code for this reason.
Constraint propagators are compound propagators whose inputs and outputs are the same, which results in bidirectional propagation:
(define (constraint-propagator name cells build)
(compound-propagator name cells cells build))Using primitive propagators for addition and subtraction, we can build
a constraint propagator for the equation a + b = c:
(define p:+ (primitive-propagator +))
(define p:- (primitive-propagator -))
(define (c:sum a b c)
(define (build)
(p:+ a b c)
(p:- c a b)
(p:- c b a))
(constraint-propagator 'sum (list a b c) build))
(define a (make-cell))
(define b (make-cell))
(define c (make-cell))
(c:sum a b c)
(add-cell-content! a 1)
(add-cell-content! c 4)
;; After the scheduler runs…
(cell-strongest b) ;; => 3With a constraint, we can populate any two cells and the propagation system will figure out the value of the third. Pretty cool!
This is a good enough propagation system for the FRP prototype.
FRP implementation
If you’re familiar with terminology from other FRP systems like “signals” and “behaviors” then set that knowledge aside for now. We need some new nouns. But first, a bit about the problems that need solving in order to implement FRP on top of general-purpose propagators:
The propagator model does not enforce any ordering of when propagators will be re-activated in relation to each other. If we’re not careful, something in the network could compute a value using a mix of fresh and stale data, resulting in a momentary “glitch” that could be noticeable in the UI.
The presence of cycles introduce a crisis of identity. It’s not sufficient for every time-varying value to be treated as its own self. In the color picker, the RGB values and the HSV values are two representations of the same thing. We need a new notion of identity to capture this and prevent unnecessary churn and glitches in the network.
For starters, we will create a “reactive identifier” (needs a better name) data type that serves two purposes:
To create shared identity between different information sources that are logically part of the same thing
To create localized timestamps for values associated with this identity
(define-record-type <reactive-id>
(%make-reactive-id name clock)
reactive-id?
(name reactive-id-name)
(clock reactive-id-clock set-reactive-id-clock!))
(define (make-reactive-id name)
(%make-reactive-id name 0))
(define (reactive-id-tick! id)
(let ((t (1+ (reactive-id-clock id))))
(set-reactive-id-clock! id t)
`((,id . ,t))))Giving each logical identity in the FRP system its own clock eliminates the need for a global clock, avoiding a potentially troublesome source of centralization. This is kind of like how Lamport timestamps are used in distributed systems.
We also need a data type that captures the value of something at a particular point in time. Since the cruel march of time is unceasing, these are ephemeral values:
(define-record-type <ephemeral>
(make-ephemeral value timestamps)
ephemeral?
(value ephemeral-value)
;; Association list mapping identity -> time
(timestamps ephemeral-timestamps))Ephemerals are boxes that contain some arbitrary data with a bunch of shipping labels slapped onto the outside explaining from whence they came. This is the partial information structure that our propagators will manipulate and add to cells.
Here’s how to say “the mouse position was (1, 2) at time 3” in code:
(define mouse-position (make-reactive-id ’mouse-position))
(make-ephemeral #(1 2) `((,mouse-position . 3)))We need to perform a few operations with ephemerals:
Test if one ephemeral is fresher (more recent) than another
Merge two ephemerals when cell content is added
Compose the timestamps from several inputs to form an aggregate timestamp for an output, but only if all timestamps for each distinct identifier match (no mixing of fresh and stale values)
(define (ephemeral-fresher? a b)
(let ((b-inputs (ephemeral-timestamps b)))
(let lp ((a-inputs (ephemeral-timestamps a)))
(match a-inputs
(() #t)
(((key . a-time) . rest)
(match (assq-ref b-inputs key)
(#f (lp rest))
(b-time
(and (> a-time b-time)
(lp rest)))))))))
(define (merge-ephemerals old new)
(cond
((nothing? old) new)
((nothing? new) old)
((ephemeral-fresher? new old) new)
(else old)))
(define (merge-ephemeral-timestamps ephemerals)
(define (adjoin-keys alist keys)
(fold (lambda (key+value keys)
(match key+value
((key . _)
(lset-adjoin eq? keys key))))
keys alist))
(define (check-timestamps id)
(let lp ((ephemerals ephemerals) (t #f))
(match ephemerals
(() t)
((($ <ephemeral> _ timestamps) . rest)
(match (assq-ref timestamps id)
;; No timestamp for this id in this ephemeral. Continue.
(#f (lp rest t))
(t*
(if t
;; If timestamps don't match then we have a mix of
;; fresh and stale values, so return #f. Otherwise,
;; continue.
(and (= t t*) (lp rest t))
;; Initialize timestamp and continue.
(lp rest t*))))))))
;; Build a set of all reactive identifiers across all ephemerals.
(let ((ids (fold (lambda (ephemeral ids)
(adjoin-keys (ephemeral-timestamps ephemeral) ids))
'() ephemerals)))
(let lp ((ids ids) (timestamps '()))
(match ids
(() timestamps)
((id . rest)
;; Check for consistent timestamps. If they are consistent
;; then add it to the alist and continue. Otherwise, return
;; #f.
(let ((t (check-timestamps id)))
(and t (lp rest (cons (cons id t) timestamps)))))))))Example usage:
(define e1 (make-ephemeral #(3 4) `((,mouse-position . 4))))
(define e2 (make-ephemeral #(1 2) `((,mouse-position . 3))))
(ephemeral-fresher? e1 e2) ;; => #t
(merge-ephemerals e1 e2) ;; => e1
(merge-ephemeral-timestamps (list e1 e2)) ;; => #f
(define (mouse-max-coordinate e)
(match e
(($ <ephemeral> #(x y) timestamps)
(make-ephemeral (max x y) timestamps))))
(define e3 (mouse-max-coordinate e1))
(merge-ephemeral-timestamps (list e1 e3)) ;; => ((mouse-position . 4))Now we can build a primitive propagator constructor that lifts ordinary Scheme procedures so that they work with ephemerals:
(define (ephemeral-wrap proc)
(match-lambda*
((and ephemerals (($ <ephemeral> args) ...))
(match (merge-ephemeral-timestamps ephemerals)
(#f nothing)
(timestamps (make-ephemeral (apply proc args) timestamps))))))
(define* (primitive-reactive-propagator name proc)
(primitive-propagator name (ephemeral-wrap proc)))Reactive UI implementation
Now we need some propagators that live at the edges of our network that know how to interact with the DOM and can do the following:
Sync a DOM element attribute with the value of a cell
Create a two-way data binding between an element’s
valueattribute and a cellRender the markup in a cell and place it into the DOM tree in the right location
Syncing an element attribute is a directional operation and the easiest to implement:
(define (r:attribute input elem attr)
(let ((attr (symbol->string attr)))
(define (activate)
(match (cell-strongest input)
(($ <ephemeral> val)
(attribute-set! elem attr (obj->string val)))
;; Ignore unusable values.
(_ (values))))
(make-propagator 'r:attribute (list input) '() activate)))Two-way data binding is more involved. First, a new data type is used to capture the necessary information:
(define-record-type <binding>
(make-binding id cell default group)
binding?
(id binding-id)
(cell binding-cell)
(default binding-default)
(group binding-group))
(define* (binding id cell #:key (default nothing) (group '()))
(make-binding id cell default group))And then a reactive propagator applies that binding to a specific DOM element:
(define* (r:binding binding elem)
(match binding
(($ <binding> id cell default group)
(define (update new)
(unless (nothing? new)
(let ((timestamp (reactive-id-tick! id)))
(add-cell-content! cell (make-ephemeral new timestamp))
;; Freshen timestamps for all cells in the same group.
(for-each (lambda (other)
(unless (eq? other cell)
(match (cell-strongest other)
(($ <ephemeral> val)
(add-cell-content! other (make-ephemeral val timestamp)))
(_ #f))))
group))))
;; Sync the element's value with the cell's value.
(define (activate)
(match (cell-strongest cell)
(($ <ephemeral> val)
(set-value! elem (obj->string val)))
(_ (values))))
;; Initialize element value with the default value.
(update default)
;; Sync the cell's value with the element's value.
(add-event-listener! elem "input"
(procedure->external
(lambda (event)
(update (string->obj (value elem))))))
(make-propagator 'r:binding (list cell) '() activate))))A simple method for rendering to the DOM is to replace some element with a newly created element based on the current ephemeral value of a cell:
(define (r:dom input elem)
(define (activate)
(match (cell-strongest input)
(($ <ephemeral> exp)
(let ((new (sxml->dom exp)))
(replace-with! elem new)
(set! elem new)))
(_ (values))))
(make-propagator 'dom (list input) '() activate))The sxml->dom procedure deserves some further explanation. To
create a subtree of new elements, we have two options:
Use something like the
innerHTMLelement property to insert arbitrary HTML as a string and let the browser parse and build the elements.Use a Scheme data structure that we can iterate over and make the relevant
document.createTextNode,document.createElement, etc. calls.
Option 1 might be a shortcut and would be fine for a quick prototype,
but it would mean that to generate the HTML we’d be stuck using raw
strings. While string-based templating is commonplace, we can
certainly do
better
in Scheme. Option 2 is actually not too much work and we get to use
Lisp’s universal templating system,
quasiquote,
to write our markup.
Thankfully, SXML already exists for this purpose. SXML is an alternative XML syntax that uses s-expressions. Since Scheme uses s-expression syntax, it’s a natural fit.
Example:
'(article
(h1 "SXML is neat")
(img (@ (src "cool.jpg") (alt "cool image")))
(p "Yeah, SXML is " (em "pretty neato!")))Instead of using it to generate HTML text, we’ll instead generate a tree of DOM elements. Furthermore, because we’re now in full control of how the element tree is built, we can build in support for reactive propagators!
Check it out:
(define (sxml->dom exp)
(match exp
;; The simple case: a string representing a text node.
((? string? str)
(make-text-node str))
((? number? num)
(make-text-node (number->string num)))
;; A cell containing SXML (or nothing)
((? cell? cell)
(let ((elem (cell->elem cell)))
(r:dom cell elem)
elem))
;; An element tree. The first item is the HTML tag.
(((? symbol? tag) . body)
;; Create a new element with the given tag.
(let ((elem (make-element (symbol->string tag))))
(define (add-children children)
;; Recursively call sxml->dom for each child node and
;; append it to elem.
(for-each (lambda (child)
(append-child! elem (sxml->dom child)))
children))
(match body
((('@ . attrs) . children)
(for-each (lambda (attr)
(match attr
(((? symbol? name) (? string? val))
(attribute-set! elem
(symbol->string name)
val))
(((? symbol? name) (? number? val))
(attribute-set! elem
(symbol->string name)
(number->string val)))
(((? symbol? name) (? cell? cell))
(r:attribute cell elem name))
;; The value attribute is special and can be
;; used to setup a 2-way data binding.
(('value (? binding? binding))
(r:binding binding elem))))
attrs)
(add-children children))
(children (add-children children)))
elem))))Notice the calls to r:dom, r:attribute, and r:binding. A cell
can be used in either the context of an element (r:dom) or an
attribute (r:attribute). The value attribute gets the additional
superpower of r:binding. We will make use of this when it is time
to render the color picker UI!
Color picker implementation
Alright, I’ve spent a lot of time explaining how I built a minimal propagator and FRP system from first principles on top of Hoot-flavored Scheme. Let’s finally write the dang color picker!
First we need some data types to represent RGB and HSV colors:
(define-record-type <rgb-color>
(rgb-color r g b)
rgb-color?
(r rgb-color-r)
(g rgb-color-g)
(b rgb-color-b))
(define-record-type <hsv-color>
(hsv-color h s v)
hsv-color?
(h hsv-color-h)
(s hsv-color-s)
(v hsv-color-v))And procedures to convert RGB to HSV and vice versa:
(define (rgb->hsv rgb)
(match rgb
(($ <rgb-color> r g b)
(let* ((cmax (max r g b))
(cmin (min r g b))
(delta (- cmax cmin)))
(hsv-color (cond
((= delta 0.0) 0.0)
((= cmax r)
(let ((h (* 60.0 (fmod (/ (- g b) delta) 6.0))))
(if (< h 0.0) (+ h 360.0) h)))
((= cmax g) (* 60.0 (+ (/ (- b r) delta) 2.0)))
((= cmax b) (* 60.0 (+ (/ (- r g) delta) 4.0))))
(if (= cmax 0.0)
0.0
(/ delta cmax))
cmax)))))
(define (hsv->rgb hsv)
(match hsv
(($ <hsv-color> h s v)
(let* ((h' (/ h 60.0))
(c (* v s))
(x (* c (- 1.0 (abs (- (fmod h' 2.0) 1.0)))))
(m (- v c)))
(define-values (r' g' b')
(cond
((<= 0.0 h 60.0) (values c x 0.0))
((<= h 120.0) (values x c 0.0))
((<= h 180.0) (values 0.0 c x))
((<= h 240.0) (values 0.0 x c))
((<= h 300.0) (values x 0.0 c))
((<= h 360.0) (values c 0.0 x))))
(rgb-color (+ r' m) (+ g' m) (+ b' m))))))We also need some procedures to convert colors into the hexadecimal representations we’re used to seeing:
(define (uniform->byte x)
(inexact->exact (round (* x 255.0))))
(define (rgb->int rgb)
(match rgb
(($ <rgb-color> r g b)
(+ (* (uniform->byte r) (ash 1 16))
(* (uniform->byte g) (ash 1 8))
(uniform->byte b)))))
(define (rgb->hex-string rgb)
(list->string
(cons #\#
(let lp ((i 0) (n (rgb->int rgb)) (out '()))
(if (= i 6)
out
(lp (1+ i) (ash n -4)
(cons (integer->char
(let ((digit (logand n 15)))
(+ (if (< digit 10)
(char->integer #\0)
(- (char->integer #\a) 10))
digit)))
out)))))))
(define (rgb-hex->style hex)
(string-append "background-color: " hex ";"))Now we can lift the color API into primitive reactive propagator constructors:
(define-syntax-rule (define-primitive-reactive-propagator name proc)
(define name (primitive-reactive-propagator 'name proc)))
(define-primitive-reactive-propagator r:rgb-color rgb-color)
(define-primitive-reactive-propagator r:rgb-color-r rgb-color-r)
(define-primitive-reactive-propagator r:rgb-color-g rgb-color-g)
(define-primitive-reactive-propagator r:rgb-color-b rgb-color-b)
(define-primitive-reactive-propagator r:hsv-color hsv-color)
(define-primitive-reactive-propagator r:hsv-color-h hsv-color-h)
(define-primitive-reactive-propagator r:hsv-color-s hsv-color-s)
(define-primitive-reactive-propagator r:hsv-color-v hsv-color-v)
(define-primitive-reactive-propagator r:rgb->hsv rgb->hsv)
(define-primitive-reactive-propagator r:hsv->rgb hsv->rgb)
(define-primitive-reactive-propagator r:rgb->hex-string rgb->hex-string)
(define-primitive-reactive-propagator r:rgb-hex->style rgb-hex->style)From those primitive propagators, we can build the necessary constraint propagators:
(define (r:components<->rgb r g b rgb)
(define (build)
(r:rgb-color r g b rgb)
(r:rgb-color-r rgb r)
(r:rgb-color-g rgb g)
(r:rgb-color-b rgb b))
(constraint-propagator 'r:components<->rgb (list r g b rgb) build))
(define (r:components<->hsv h s v hsv)
(define (build)
(r:hsv-color h s v hsv)
(r:hsv-color-h hsv h)
(r:hsv-color-s hsv s)
(r:hsv-color-v hsv v))
(constraint-propagator 'r:components<->hsv (list h s v hsv) build))
(define (r:rgb<->hsv rgb hsv)
(define (build)
(r:rgb->hsv rgb hsv)
(r:hsv->rgb hsv rgb))
(constraint-propagator 'r:rgb<->hsv (list rgb hsv) build))At long last, we are ready to define the UI! Here it is:
(define (render exp)
(append-child! (document-body) (sxml->dom exp)))
(define* (slider id name min max default #:optional (step "any"))
`(div (@ (class "slider"))
(label (@ (for ,id)) ,name)
(input (@ (id ,id) (type "range")
(min ,min) (max ,max) (step ,step)
(value ,default)))))
(define (uslider id name default) ; [0,1] slider
(slider id name 0 1 default))
(define-syntax-rule (with-cells (name ...) body . body*)
(let ((name (make-cell 'name #:merge merge-ephemerals)) ...) body . body*))
(with-cells (r g b rgb h s v hsv hex style)
(define color (make-reactive-id 'color))
(define rgb-group (list r g b))
(define hsv-group (list h s v))
(r:components<->rgb r g b rgb)
(r:components<->hsv h s v hsv)
(r:rgb<->hsv rgb hsv)
(r:rgb->hex-string rgb hex)
(r:rgb-hex->style hex style)
(render
`(div
(h1 "Color Picker")
(div (@ (class "preview"))
(div (@ (class "color-block") (style ,style)))
(div (@ (class "hex")) ,hex))
(fieldset
(legend "RGB")
,(uslider "red" "Red"
(binding color r #:default 1.0 #:group rgb-group))
,(uslider "green" "Green"
(binding color g #:default 0.0 #:group rgb-group))
,(uslider "blue" "Blue"
(binding color b #:default 1.0 #:group rgb-group)))
(fieldset
(legend "HSV")
,(slider "hue" "Hue" 0 360 (binding color h #:group hsv-group))
,(uslider "saturation" "Saturation" (binding color s #:group hsv-group))
,(uslider "value" "Value" (binding color v #:group hsv-group))))))Each color channel (R, G, B, H, S, and V) has a cell which is bound to
a slider (<input type="range">). All six sliders are identified as
color, so adjusting any of them increments color’s timestamp.
The R, G, and B sliders form one input group, and the H, S, and V
sliders form another. By grouping the related sliders together,
whenever one of the sliders is moved, all members of the group will
have their ephemeral value refreshed with the latest timestamp. This
behavior is crucial because otherwise the r:components<->rgb and
r:components<->hsv propagators would see that one color channel has
a fresher value than the other two and do nothing. Since the
underlying propagator infrastructure does not enforce activation
order, reactive propagators must wait until their inputs reach a
consistent state where the timestamps for a given reactive identifier
are all the same.
With this setup, changing a slider on the RGB side will cause a new color value to propagate over to the HSV side. Because the relationship is cyclical, the HSV side will then attempt to propagate an equivalent color value back to the RGB side! This could be bad news, but since the current RGB value is equally fresh (same timestamp), the propagation stops right there. Redundant work is minimized and an unbounded loop is avoided.
And that’s it! Phew!
Complete source code can be found here.
Reflections
I think the results of this prototype are promising. I’d like to try
building some larger demos to see what new problems arise. Since
propagation networks include cycles, they cannot be garbage collected
until there are no references to any part of the network from the
outside. Is this acceptable? I didn’t optimize, either. A more
serious implementation would want to do things like use case-lambda
for all n-ary procedures to avoid consing an argument list in the
common cases of 1, 2, 3, etc. arguments. There is also a need for a
more pleasing domain-specific language, using Scheme’s macro system,
for describing FRP graphs.
Alexey Radul’s dissertation was published in 2009. Has anyone made a FRP system based on propagators since then that’s used in real software? I don’t know of anything but it’s a big information superhighway out there.
Update: Since publishing, I have learned about the following:
Holograph: A visual editor for propagator networks! Amazing!
Scoped Propagators: A WIP propagator system with some notable differences from “traditional” propagators.
I wish I had read Alexey Radul's disseration 10 years ago when I was first exploring FRP. It would have saved me a lot of time spent running into problems that have already been solved that I was not equipped to solve on my own. I have even talked to Gerald Sussman (a key figure in propagator research) in person about the propagator model. That conversation was focused on AI, though, and I didn’t realize that propagators could also be used for FRP. It wasn’t until more recently that friend and colleague Christine Lemmer-Webber, who was present for the aforementioned conversation with Sussman, told me about it. Christine has her own research project for propagators. There are so many interesting things to learn out there, but I am also so tired. Better late than never, I guess!
Anyway, if you made it this far then I hope you have enjoyed reading about propagators and FRP. ’Til next time!